top of page

​Incentre

  • Discover the Properties of Incentre

  • Application on Questions

  • Find the Coordinate of Incentre

angle bisector.png

Pre-Class Observation

  • Try to Guess where will three angle bisectors intersect

  • Drag the vertices or click randomize to rearrange the triangle

  • Is there anything you notice?

Where Centre" locates?
Imagine the Change when you move vertices

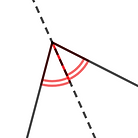
Intersection of Angle Bisectors:

  • The intersection point of all the three interior angle bisectors of the triangle is the incentre

Incentre: Green Point

Properties of the Incentre of Triangle​

  • Incentre always lies inside the triangle.

  • The sides of the triangle are tangents to the inscribed circle​

​

  • I is the incentre (angle bisector)

    • ∠BAI = ∠CAI

    • ∠BCI = ∠ACI

    • ∠ABI = ∠CBI

​

  • I is the incentre Equal distance sides 

    • AE = AG

    • CG = CF

    • BF = BE​

​

  • Properties of angle bisector:
    • For any angle bisector cutting a triangle into two:

      • AB : BC = AB' : B'C

      • AB : AC = A'C : A'C

      • BC : AC = BC' : AC'

Incentre prop.png

Furthur Explore

  • Try to check the properties

  • Can you notice the properties above?

Application

IC1_edited.jpg
Question 1
Question 2
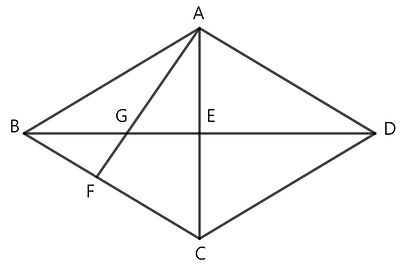
IC2_edited.jpg
Question 3
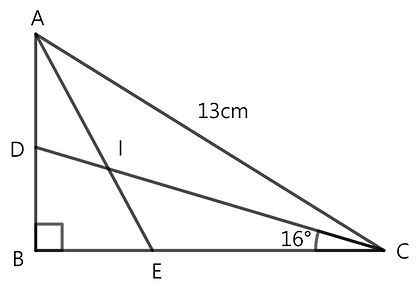
IC3_edited.jpg
IC4_edited.jpg
Question 4

Incentre :
Coordiante Geometry

How to Find &

Relation with Inscribed Circle

Incentre Formula

Incentre Proof.png
incentre formula.png

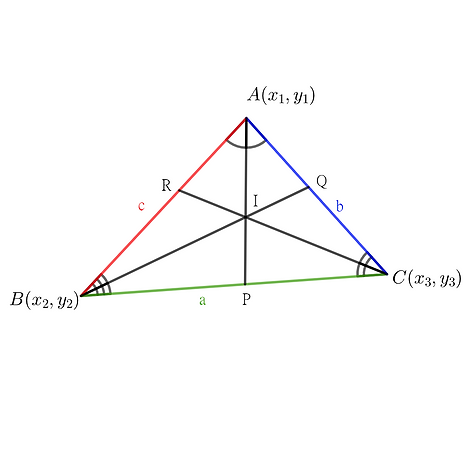
Proof

五顏六色的書籍

Practice Time

Capstone Project:

Learning Package for Triangle Centers
-5E instructional model

bottom of page