top of page

Centroid

  • Discover the Properties of Centroid

  • Application on Questions

  • Find the Coordinate of Centroid

median.png

Pre-Class Observation

  • Try to Guess where will three medians intersect

  • Drag the vertices or click randomize to rearrange the triangle

  • Is there anything you notice?

Where Centre" locates?
Imagine the Change when you move vertices

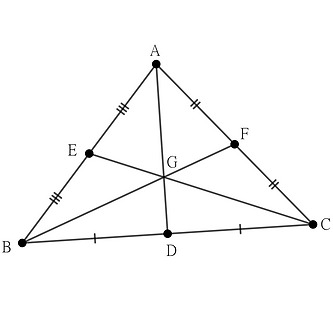
Intersection of Medians:

  • The line segments of medians join vertex to the midpoint of the opposite side.

  • All three medians meet at a single point. The point is known as the Centroid of a triangle.

Centroid Blue Point

Properties of the Centroid of Triangle

  • The centroid is always inside the triangle

​

  • Each median divides the triangle into two smaller triangles of equal area.

​

  • ​Centroid divides each median into two parts. The ratio of shorter side to longer side is always 1 : 2​

    • GD : GA = 1 : 2

    • GF : GB = 1 : 2

    • GE : GC = 1 : 2

Centroid prop.png

Furthur Explore

  • Try to check the properties

  • Can you notice the properties above?

Application

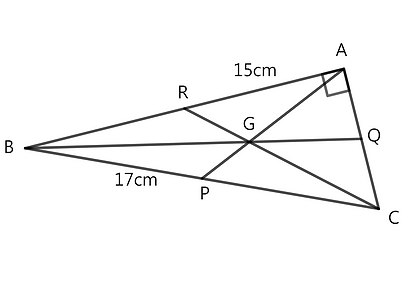
C1.png
Question 1
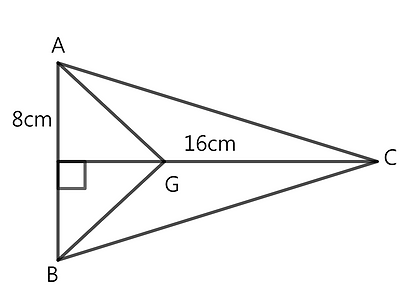
Question 2
C2.png
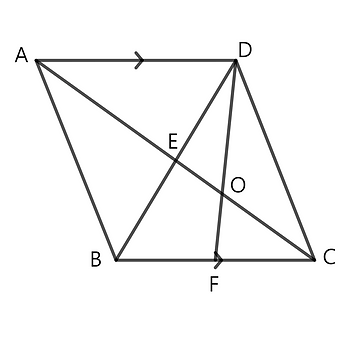
C3.png
Question 3
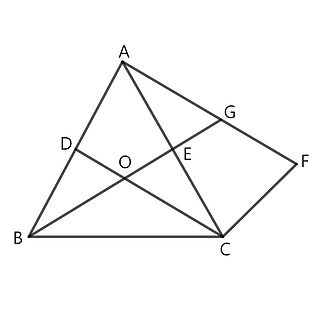
C4.png
Question 4

Centroid :
Coordiante Geometry

How to Find &

Relation with Section Formula

Centroid Formula

Centroid Proof triangle.png
Centroid formula.png

Proof

五顏六色的書籍

Practice Time

Capstone Project:

Learning Package for Triangle Centers
-5E instructional model

bottom of page